Multiplying large numbers is difficult. Any 4th grade math student will tell you that! When you learned how to multiply large numbers, it probably looked a little like this. Personally I never liked the way we were taught to multiply numbers, because the multiplication was complicated with steps of addition. After that everything is added again. It’s rubbish.
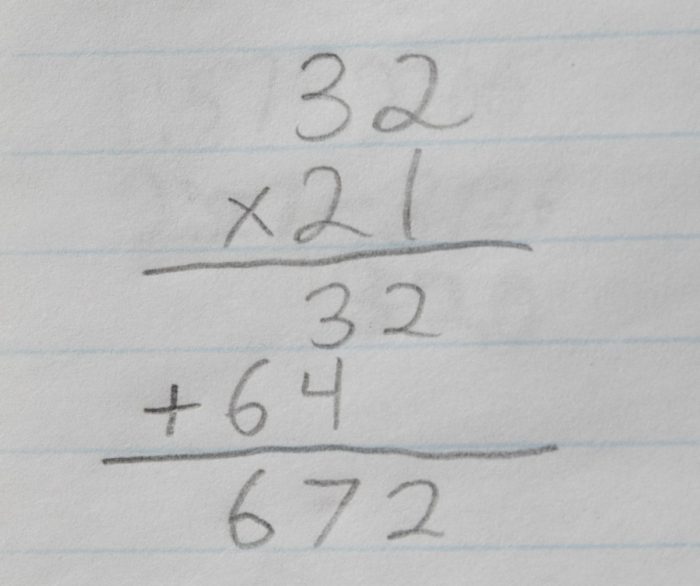
This is complicated because larger numbers require you to carry digits over to the next column.
There has to be a better way! There is.
Line Multiplication is a visual method to multiply numbers by drawing lines and counting the intersections. Intersections are added up for the proper result. This simplifies the multiplication into one step (no carrying numbers) and addition in another. The lines can replaced with a matrix, eliminating drawing and counting.
Line Multiplication
Line multiplication is a trick that allows you to multiply numbers by simplifying and visualizing the problem. In this method, lines are drawn for each digit of each number.
In this case, we will use 32 x 21. One number will be represented with vertical lines, the other will have horizontal lines.
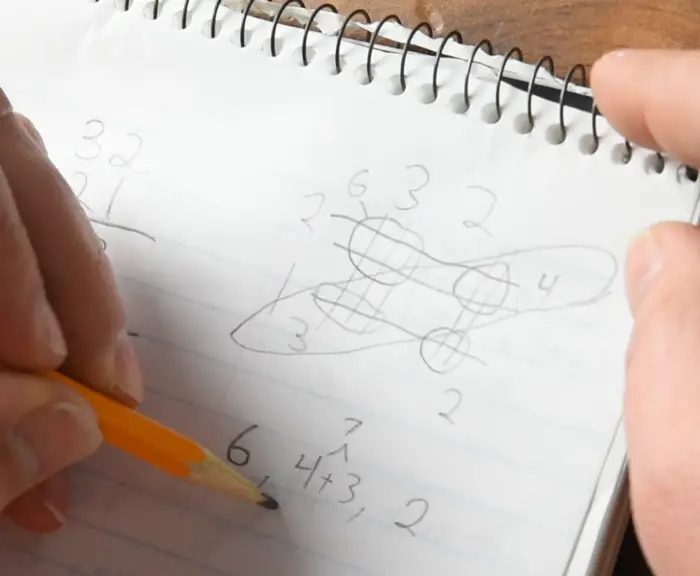
The real trick is in how the counting is done. We will count up each group of line crossings. When we count the intersections, we get 6, 4, 3, 2, when we count left to right and then top to bottom.
We will then divide these into three categories representing the ones, tens and hundreds group. The top left section will go in the hundreds category, and the bottom right will go in the ones category. The other two groups will be combined in the tens category. These are the diagonal groups.
| Hundreds | Tens | Ones |
| 6 | 4, 3 | 2 |
We will then write out the solution of combining (addition) any single groups and then smooshing them together. In our example it is 6, 4+3, 2 or 672. A quick check with a calculator may be necessary for you to believe. Believe!
This is a great trick, because it relies less on complicated multiplication and more on simple addition. But it has three main setbacks that impede its widespread use. I’m hoping to change that.
Problems with Line Multiplication
Numbers with 0
The question here is how do you draw 0 lines? If you want to multiply 103 x 462, how do you keep those straight? You can leave a space on the paper and hopefully you will remember there is a gap. Another alternative is to use a different color line to represent a 0 and then not count them for the result.
Numbers That Multiply to Greater Than 9
You can see from the example of 32 x 21, that none of the individual numbers can multiply to greater than 9. This was by design so that you wouldn’t be confused early on. The method still works for numbers greater than 9, but it does take some knowledge of how to deal with them.
Large Digits
Drawing out more lines than 5 or 6 gets tedious. Furthermore, who wants to count the 72 crossing when 8 and 9 lines intersect. Count me out. This is the very reason we learn multiplication in the first place.
Improving Line Multiplication
Hopefully, by now we can see the line multiplication reduces the complexity of the multiplication to what we learned in our times tables. We also shift to using more addition. There is no argument from me that addition is much simpler than multiplication.
I think that the real simplification comes from having a clear separation between the addition and multiplication steps.
So how do we get eliminate the complexities of line multiplication and get it to where the process is useful. Simple, we eliminate the lines!
When I drew the lines for 32 x 21, I realized that we were really just making a matrix of simple multiplication. If we change our thinking from drawing lines to making a matrix, we can eliminate the drawing and counting. That’s a huge time saver.
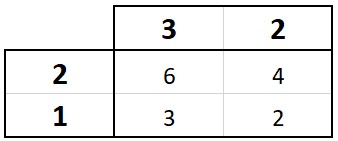
This solves the problems of numbers with 0 because a “0” in the matrix would give a row or column of zeros. Also, doing the multiplication eliminates the need for counting large numbers in a group.
When using the matrix, the diagonals are any squares where only the corners touch when moving from bottom left to top right.
Adding Number Larger Than 9
The trick to adding numbers larger than 9 is how they are placed in the addition step. To explain this, we will use the example of 92 x 36.
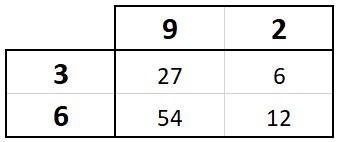
Creating the matrix we get the following. As you can see, I’m glad we didn’t use lines for 9 x 6. I don’t want to spend the time counting something I already know the answer to.
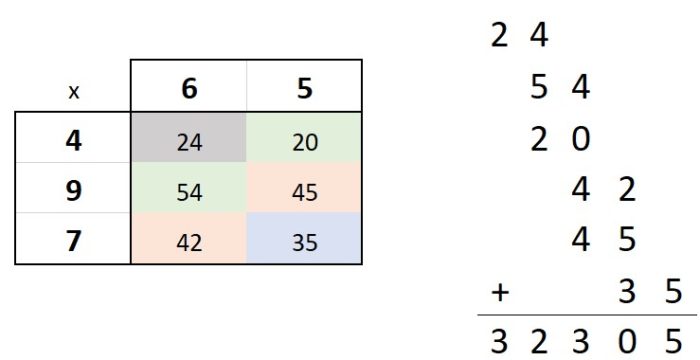
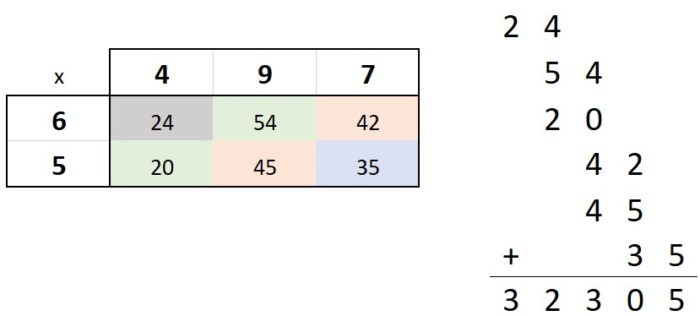
The trick is remembering which group each number belongs in and keeping it in the right order. The ones group is 12, the tens group is 54 and 6 and the hundreds group is 27. For each group we (right) indent one digit and then add together.
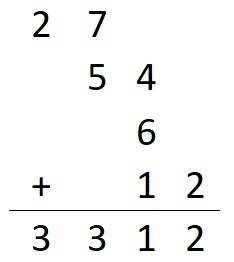
You can see the the 12 was placed in the bottom right, with the 6 and the 4 in 54 above the 1 (one indentation for the tens). The 7 in 27 was placed above the 5 (two indentations for the hundreds). Then we add like any other math problem.
Three (Or More) Digit Numbers with Zero
You may be asking, “What do I do about larger numbers?” The answer is keep adding the diagonals up together. No matter how large the matrix formed is, you will separate the diagonals into categories. Each diagonal is counted as you move from bottom right to top left will add another category of to the solution (This is the one, tens, hundreds….). Each element in a category must touch at the corners.
Let’s work through the example of 103 x 462. When the matrix is filled, we have an entire column of “0” because of the “0” in 103.
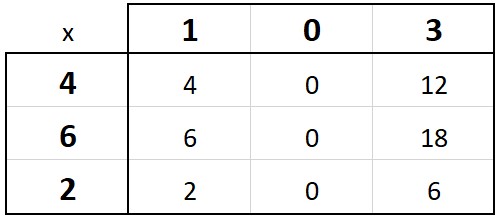
Since we have 3 digit numbers, we will have a 3 x 3 matrix. As a result, we will increase from 3 categories in the 2 x 2 matrix to 5. We will now have a thousands and ten thousands category.
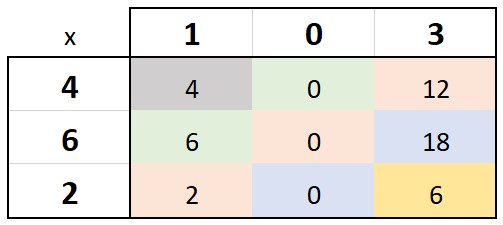
| Category | Numbers |
| Ones (yellow) | 6 |
| Tens (blue) | 0, 18 |
| Hundreds (peach) | 2, 0, 12 |
| Thousands (green) | 6, 0 |
| Ten Thousands (gray) | 4 |
It is at this point that we can start to add things up. We have two unique things that are happening, but don’t get worried. First, we are going to ignore the zeros. Second, when there are no digits to carry over, we will add them in the same line.
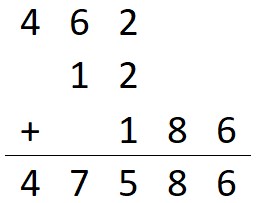
You can see that three times we added numbers to the same line because there were no digits to carry over. The first time was placing the 18 right in front of the 6 for the ones and tens category. The second and third time was placing the 6 (thousands) in front of the 2 (hundreds) and the 4 (ten thousands) in front of the 6.
Unequal Digit Multiplication
So far, we have only done examples when the factors (numbers being multiplied) are of equal digits. Often, you will have factors of unequal digits and we need to know how to deal with that.
Using the example of 65 x 497, we have a 2 digit and a 3 digit factors and will end up with a 2 x 3 or 3 x 2 matrix. The process still holds up and it doesn’t matter which factor is horizontal or vertical. We will still divide the diagonals in to the appropriate category and then add them together.
In either case (see problems worked out below), we end up with the tens diagonal containing 42 and 45. The hundreds diagonal will have 20 and 54.
Conclusion
As you can see, line multiplication is an interesting concept, but has a few short falls: drawing “0” lines, carrying digits and counting numerous crossings. Transitioning from lines to a matrix, simplifies the process. Here is a summary of the process.
- Arrange the factors with one horizontal and one vertical
- Fill in the matrix by multiplying each digit in each number. (Should never be higher than 81)
- Starting with the bottom right corner, divide the matrix into categories of ones, tens, hundreds, etc. This is done on a diagonal from bottom left to to top right where the terms must touch corner to corner.
- Starting with the ones category, begin to add the digits. As each new category is introduced, it must be indented one digit from the right.
- Add to get your solution.
Using the matrix solution allow one to quickly and easily multiply large numbers. It is a great tool and I am surprised that it is not taught in school.

