Planetary gearboxes offer three distinct advantages over other gearbox types: high ratios of reduction, higher torque transmission and inline motion transfer.
Achieving high ratio planetary gear boxes is done using multiple gear sets. The speeds of each item are related through the following formula: -S/R = (ωr-ωa)/(ωs-ωa). There are two different methods depending on the torque transmitted and if the desired output is the ring or arm.
Before going further, if you are new to planetary gear sets, you may want to read this article first before continuing to learn how the gear ratios are calculated.
Sun Input – Carrier Output
Having the sun as an input and using the carrier as an output is a good way to gain medium ratio gearboxes. In a single planetary gear set, having a 10:1 ratio is around the practical maximum in this configuration.

Although higher ratios are possible, the size gets to be really big and it is wiser to use multiple sets of planetary gears to achieve high ratios. If you use two 10:1 gear ration in series where the carrier output of Section 1 is now the sun input to Section 2 a 100:1 ratio is easily achievable.

Let’s look at this drill as an example. Between the motor and the chuck, there is a 36:1 ratio planetary gearbox. Not only does the gearbox increase the torque capacity and allow the motor to turn at its optimal speed, it also provides a mechanism limit torque.
When disassembled, there are two sets of gears using the same ring gear. The sun has 9 teeth, ring 45 teeth and planets 18 teeth. The ring stays locked most of the time. However, when the torque is higher than its desired setting, it will slip causing no motion in the system.

It can slip because there are tabs on the opposite side to the ring that are mated in a track with ball bearings. The track has a spring that presses the ball bearings between the tabs. When the torque exceeds the setting, the spring will compress allowing the balls to pass over the tabs. This allows the ring to rotate.
Using the universal planetary gear equation, we can see that if we input 1 revolution on the sun and hold the ring steady, we get 0.166 revolutions on the output. This is a 6:1 ratio.
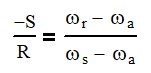
When the carrier output is connected to the sun on the next section, we repeat the process and get another 6:1 ratio reduction. We can calculate the entire ratio by using the series of equations below.

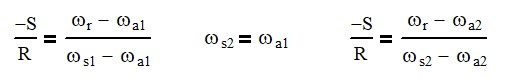
Sun Input – Ring Output
If you want ratios that are even higher, you will need to have a sun input and a ring output. The gearboxes above could utilize the same ring for each gear section. To achieve higher ratios, you would need to have these be different.
In the first section, the ring will be fixed and the sun will be the input, the output will be the planets and not the carrier. In fact, in the example below, there is no planet carrier.
In the first section, we will need to use the universal planetary motion equation (eq. 1) to calculate the speed of the arm (important even if there is no carrier). We will also need to calculate the planet motion using equation 2 below.
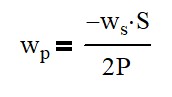
The second section, the planets provide the input and the ring is the output. Here there is no sun gear, although there could be, simply to balance reactive forces between the planets and ring. It is also important to note that the Arm distance must be the same on both sections.
Since the planets are driving, Equation 1 won’t work. We instead need to use Equation 3 to find the ring output motion, wo. From there, we could use Equation 1 to find the speed of the sun in Section 2.
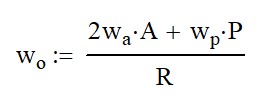
Example: 160:1 Winch Reduction

On YouTube, “Gear Down for What?” made a video where they 3D printed a 160 to 1 winch and used it to lift an obscene amount of weight. I wanted to break that winch down for you and show how the planetary gears used allow for that.
The winch is constructed with three sections of planetary gears. The left and right are the input and have the same gearing. The ring is held stationary because it can be held stationary from a lifting point
The middle section is the output, it has a scallop in it to guide the rope as it winds.

We find in the the right and left sections (Section 1), that there are 27 teeth on the sun, 45 teeth on the ring and the 9 planets have 9 teeth each. To illustrate our ratio, we will have the sun input turn at 160 rpm so that we will get 1 rpm out.
If you watch the video, you will notice that these teeth are not cut as spur gears, but as helical gears in a V shape. This gives two advantages. First, the helical gears will run quieter. Second, the V shape allow the planets to stay in place without using a carrier.

Using Equation 1, we find that the carrier output is 60 rpm. We can also use Equation 2 to find that the planets will turn -240 rpm.
Using Equations 3 and 4 we can iterate to find the output speed of 1 rpm. It is a little tricky because if we assume the same diametric pitch between Sections 1 and 2, we would need a 8.81… tooth planet and a 44.81… tooth ring to get a 160:1 ratio. It should be obvious that only an integer number of teeth will mesh.
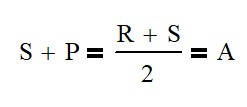
So what do we do?
Scaling for Diametric Pitch Changes
We can see from the picture of the winch that the gear teeth in the center are much smaller than on Section 1 indicating an increase in diametric pitch.
We will need to keep the arm diameter the same in both cases in order to work. We can use the following equation to scale up the diametric pitch and still keep the proper carriage size.
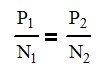
Where P is the gear diametric pitch and N is the number of teeth on the gear. Using equation 4, we can determine A would have 18 teeth. Looking at the picture, I would assume that Section 1 has a diametric pitch of 6.
We can use Equation 5 to determine the number of teeth needed for the carrier arm if we changed to a 32 diametric pitch. Using cross multiplication, we would find that the carrier would have 96 teeth.
Using the three equations below, we can have wr = 1 revolution and then solve for S, P and R. Here we would find that R = 239, S = 145 and P = 47.
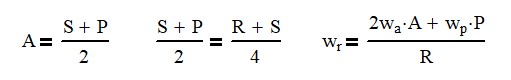
Since I’m guessing at what the diametric pitch that these guys are using, these numbers may not be accurate and there may be other options to get you close to a 160:1 ratio. I found that using an Arm of 47 got you to a 156:1 ratio but you will not find gears on a shelf with that diametric pitch.
Conclusions
Planetary gears offer a variety of methods to achieve high reduction ratios using very few gears. This allows for high torque transmission and the ability of a relatively small motor lifting heavy weights.
The calculations shown here are can be used in multiple ways to determine exactly what any part of the system is doing.
*Feature image courtesy of “Gear Down for What?” video on a 160:1 planetary gear set.

