Many engineers see calculus as just a gateway to getting an engineering degree but it is so much more. Calculus is the math of the universe, explaining how all things interface together. Calculus is the foundation to even begin to understand physics, thermodynamics, materials, fluid mechanics, electronics and statistics. Without calculus, mechanical engineering wouldn’t exist!
At this point, everyone rolls their eyes at me.

For me, I have designed nearly 100 different machines or machine subsystems. I can honestly say that I have performed calculus only 6 times on the job. Five of the six had to do with beam deflection and a seventh was used to determine if my water heater capacity was enough. (I know, I’m a nerd.) However, I have used the premises of calculus hundreds of times in design. Often times, the work of calculus has already been defined in tables. Whoo hoo!
History of Calculus
Calculus has it’s reaches back to ancient days as far back as the fifth century BC when mathematicians like Eudoxus tried to estimate the volume of shapes by dividing them into smaller and smaller shapes. The reason for small shapes is they are easier to calculate. He called this the ‘method of exhaustion’. We call this the ‘limit’ in modern calculus.
Archimedes was the first to pioneer integral calculus which he called ‘heuristics’ and use that to find the area of the circle by inscribing a many sided polygon. He found that as the number of sides increased it more and more approximated the area of the circle.

Modern Calculus
After these ancient discoverers passed on, calculus, sat dormant until the 17th century. At this point, Sir Isaac Newton and Gottfried Wilhem von Leibniz went on to formalize derivative calculus as we know it now. Surprisingly they worked on this separately each without knowledge of the other.

Isaac Newton studied why objects fall at an increasing rate of speed every second and why the celestial bodies will always orbit in an elliptical shape. He knew there was something behind these and needed a mathematical way of explaining it.
After mapping how an object falls over time he noticed that the curve was not linear and it kept increasing. He needed a way to find out what the velocity was at any given time.
Looking a distance vs time chart, he knew that if you drew a secant line near the point of interest, he could get a close approximation of the velocity. As the secant became smaller and smaller in length, will he get closer and closer to the tangent. The slope of the tangent line is the velocity.
This process above is known as derivative calculus. This is where we can find the slope at any point of any curve. In his research Newton found that the opposite of the derivative is the integral and that all of the information needed in a definite derivative could be switched back to an integral. This is also true and reverse.

Leibniz and Newton’s developed and published their works separately and both had come up with integral and differential calculus at different times. In their publications, both of the mathematicians use different terminology but came up with the same fundamentals.
Two this day both terminologies of calculus are still used. Newton would puts a dot over the variable when a derivative was taken. For every derivative there were be another dot placed. Another alternative to the dot is to put an apostrophe afterward for each derivative. Leibniz uses the more traditional notation with the integral sign and the dx (or whatever the dependent variable is) after the integral.
What is Calculus?
Calculus can be divided into two parts: the derivative and the integral. The derivative is the slope of a curve at any one point. The integral is the area under the curve over a given range.
Before we can dive into those topics, we need to discuss the limit first.
The Limit
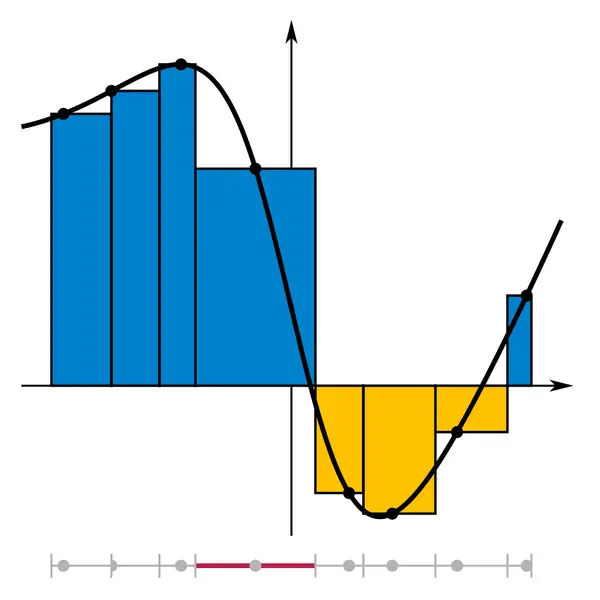
The limit is the process of dividing a function or equation into chunks. The smaller the chunks are, the better accuracy. For example, if we want to estimate the area of a circle by inscribing an equilateral triangle in it, you will have a very bad approximation of the area. As you increase the sides to 6 (a hexagon), your approximation gets better. If you go to a million sided polygon, your approximation is very good.
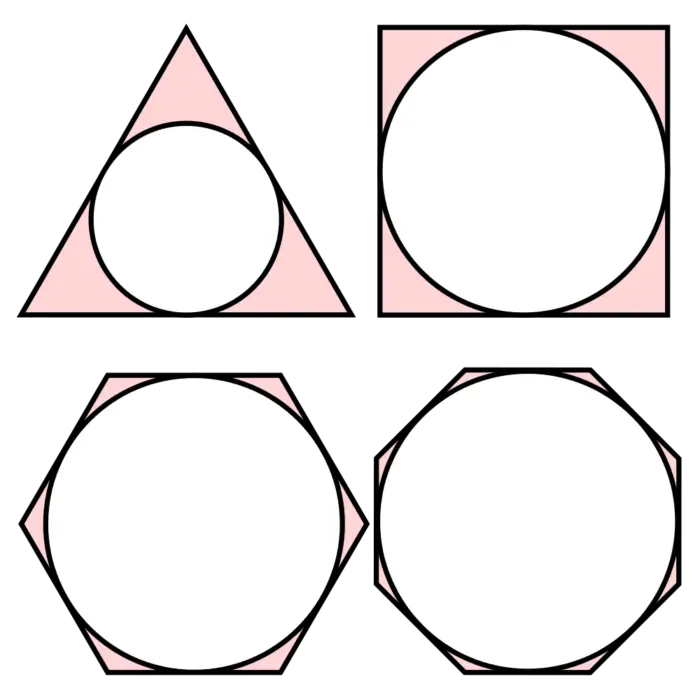
Image Courtesy of Braindrain0000
Another example of a limit is in (American) Football. If the offense is on the 25 yard line and the defense is penalized for ‘unsportsmanlike’ conduct (normally a 15 yd penalty), the ball will be placed half the distance to the goal on the 12.5 yard line and not the 10 yard line. If the defense keeps getting penalized every play, the ball will move closer to the goal line by half each time; 6.3, 3.3, 1.6, 0.8, 0.4, 0.2 etc.
The main thing to keep in mind here is no matter how many times the defense is penalized, the offense will never score. However, as the defense does get penalized, the offense gets a little closer to the intended “limit.”

If we look at the equation below, we can see that the value of y when x = 0 is 0/0 or undefined. However, if we move just slightly to the right (or left) we see that the value of y is just less than 1.
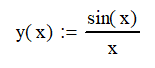
This is where the limit concept shines, we can find out values of functions at points that don’t really exist. The graph below shows the function from x = 0 to 10. You can see that as x approaches 0 from the right, the value of y is 1.
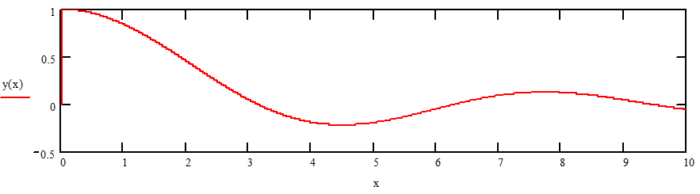
In calculus terms, we would express this as, “What is the limit of y, as x approaches 0.” If it is a discrete equation, you may need to evaluate the function “from the left” (meaning x values increasing) and / or “from the right” ( x values decreasing) to get the right answer.
Limits allow us to divide the function into smaller and smaller chunks of the function to evaluate things like slope and area.
Now let’s get on with the two parts of calculus!
The Derivative
The derivative where one can find the instantaneous slope or tangent of any mathematical function. This is great if we have a position vs. time chart and want to find the velocity (tangent) at any point. We can take multiple derivatives and find the acceleration (2nd derivative) and jerk (3rd derivative, yup its a real thing) of a function as well.
In any mathematical function, the derivative is found by taking a secant on the curve near the point in question. A secant is a line made through two points on a curve. Our interest in the secant is simple; it is very easy to find the slope of a line (rise / run). The points selected can be anywhere over the graph.
If we had a graph of the Dow Jones Industrial Average over the last 20 years, we might pick the points of today and 20 years ago and draw our line. We will probably find that the line slopes up.
If we are a stock analyst, this just won’t cut it because it is to general of an estimation. We probably want to look at the trend of the market between right now, and 5 yr, 1 yr, 1 mo, 1 wk, 1 day, 1, hr and 5 min. This will give us an good approximation of what the market is about to do.
We can then calculate the slope of the line for each secant and determine if the market is going up down or sideways.
Hopefully you noticed that our secant line got smaller and smaller in each step as we approach an infinitesimally small length of the secant line. As the length of the line approaches zero, the line will more and more represent a tangent line. This is what the derivative is.
There are many tables that have the derivative function for many common equation forms. These will have generic constants so that they able to be used in a wide variety of applications
The Integral
The other part of calculus is integration; this is where we can find the area under any curve. This is used if we had a plot of acceleration over time we could integrate to find the unit the velocity and then integrate again to find distance.
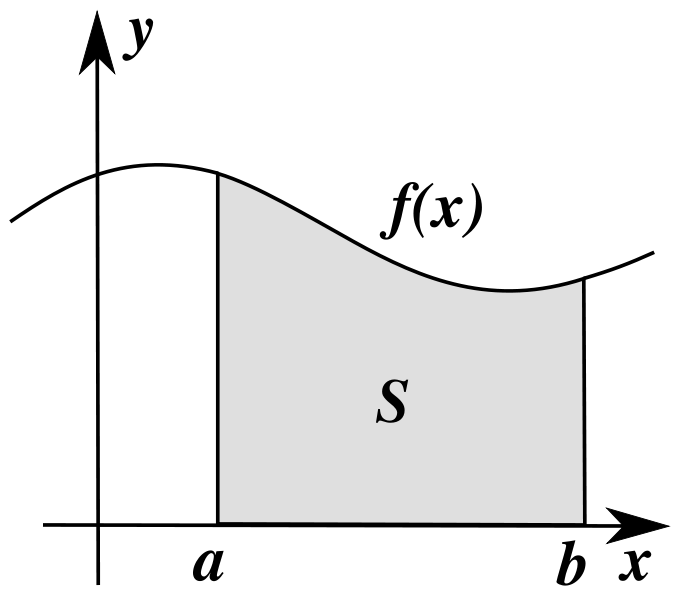
By dividing the area under the curve into smaller rectangular approximations, we can approximate the total area. As the number of rectangles increases, the accuracy of the result increases.
Quick shortcut: if you need to find the integral of a very difficult function, plot it out on paper. Then cut out the shape and weigh it. Compare this weight with a full sheet of paper. If you don’t have a scale that can read that small of a mass, you could also cut it on a laser metal cutter or print it in 3D.
Definite vs Indefinite Integrals
Not all integrals are created equal, there are two types; definite and indefinite. A definite integral has two points, 1 and 4 in the case below case, to evaluate after the integration is complete. The definite integral will always give a specific value as a result.
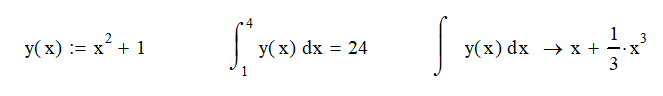
The indefinite integral is a little more fun. It doesn’t have a specific set of bounds so it gives a function (see right) instead of a specific value. With an indefinite integral, you will also have a constant, usually C, on the end of the integrated function. If there are multiple integrations done, the constants, C, would have subscripts (i.e. C1, C2 …Cn).
Once you get this far, we need to start applying boundary conditions to get the result we would like. In the equation above, we would only need 1 boundary condition.
When dealing with beam deflection, you need to integrate twice so you would have two constants C1 and C2. As a result, you would need two boundary conditions per beam section. If this were a simply supported beam, we would say that the deflection at x=0 is 0 in and x=L is 0. These are our boundary conditions
Studies Past Calculus
Multidimensional or multivariable calculus is the next step, we may want to see how the function changes with respect to x, y, z, and time. Aeronautics is a great application of multivariable calculus as we need to know how fluid flows around an airplane wing.
Differential equations is also a must for the engineer. Differential equations are how we study radioactive decay, vibrations, electronics and how long you can shower before your water gets cold.
Differential equations is broken down into two sections, ordinary and partial. Ordinary Diff Eq, deals with only one dependent variable at a time while Partial Diff Eq deals with multiple variables. I did not enjoy this class at all.
Why Calculus is Important
Hopefully, it is plain to see that knowing the area under a curve for the slope and of a curve at any point is very important to an engineer. If you still don’t believe me here are some examples.
Meteorology -meteorologists use calculus to determine how wind will flow between a high and low pressure areas. As a high pressure area will force air to move to a low pressure area. We can determine the size and shape of these areas and determine how windy it will be.
In physics, calculus explains how motion is controlled. We know that that the motion of a car can not instantaneously change position the velocity but motion speeds up and slows down gradually. Calculus is the tool that allows us to mathematically model motion.
Calculus is widely used in rocket propulsion. First at lift off, the rocket has a constantly changing weight because it keeps burning off fuel. Right at lift off, you need to burn more fuel than when you are near orbit. Calculus is also used to determine the gravity force as the rocket is further and further from earth. Finally, determining the speed and height from earth needed for an infinite orbit is found using, you guessed it, calculus.

In structures we know that a suspension bridge is held up by cables that have a constantly changing slope. It is difficult without calculus to determine what the tension is on the cable at any point.
As mentioned, beam deflections are based off of the universal beam equation and requires a double integral for a solution.
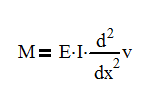
In electronics, we know that capacitors and inductors cannot charge or discharge instantaneous. Calculus is our bridge to understanding how fast a capacitor will charge. This is important to know because it affects switching speeds. If a capacitor takes 1s to go from 0V to 5V. We can only pass a 1 Hz signal through. If it takes, 1 ms, we can send a signal of 16 Hz.
Calculus also explains how heat will transfer through walls, fluids and in space. Coroners use the normal and actual temperature of a body as well as the ambient temperature to determine the time of death.
Fluid mechanics uses multivariable calculus and partial differential equations to govern all fluid motion using the Navier-Stokes equations. While these long and tedious equations can be approximated and simplified, all Computational Fluid Dynamics (CFD) is based off them and allows us to model fluid flow through many complex shapes like the inside of a hydraulic valve or airflow over an airplane wing.

Other examples are in statistics where we can use normal distribution to gain confidence in how well our sample sizes represent reality. This is all calculus based. In economics, we use calculus to find optimum profitability in sales, supply and inventory.
In Summary
I have only scratched the surface on how calculus is used in real world everyday situations. Calculus is truly the natural language of the universe and understanding it will only lead to greater awe of this world we live in.


